TÍTULO: Movimiento Rectilíneo Uniformemente Acelerado
CRITERIOS EVALUADOS: C
|
7-8
|
El alumno es capaz de:
i. Obtener, organizar, transformar y presentar correctamente los
datos en formatos numéricos o visuales
ii. Interpretar los datos con exactitud y explicar los
resultados mediante un razonamiento científico correcto
iv. Evaluar la validez del método según el resultado de una
investigación científica
v. Explicar mejoras o ampliaciones del método que beneficiarían a
la investigación científica
|
·
El alumno registra en una tabla correctamente formateada (título y
columnas rotuladas con las magnitudes y unidades) los datos brutos y/o
procesados obtenidos en el laboratorio.
·
Los cálculos numéricos necesarios son correctos y el alumno pone un
ejemplo de los mismos.
·
El alumno extrae una conclusión principal a partir de la correcta
interpretación de los resultados.
·
La conclusión se argumenta con comentarios sobre la precisión y exactitud
de los resultados, y si procede, de la diferencia porcentual entre el valor
obtenido y esperado.
·
El alumno establece la validez del método utilizado, sopesando
·
las implicaciones del mismo y sus limitaciones (precisión, exactitud,
etc.), a partir de la correcta interpretación de los resultados.
·
El alumno expone detalladamente dos o más posibles debilidades o
fuentes de error de los resultados no triviales relacionados con el método
empleado.
·
El alumno expone detalladamente mejoras realistas para cada una de
las debilidades mencionadas y/o ampliaciones del método que redundarían en
una mejor investigación.
|
OBJETIVO: Estudiar experimentalmente la posición y velocidad de un móvil
con aceleración constante en función del tiempo.
INTRODUCCIÓN TEÓRICA:
Un cuerpo abandonado sobre un plano, inclinado un
ángulo respecto a la horizontal, se mueve con movimiento rectilíneo
uniformemente acelerado (MRUA en adelante). Ello es debido a la componente
paralela al plano de la aceleración de la gravedad.
Como s = ½·a·t2, la aceleración, a = 2s/t2, puede hallarse en función de los desplazamientos y de los tiempos tardados, y su valor debe ser, dentro de un margen de error, aproximadamente constante.
Como s = ½·a·t2, la aceleración, a = 2s/t2, puede hallarse en función de los desplazamientos y de los tiempos tardados, y su valor debe ser, dentro de un margen de error, aproximadamente constante.
Por otra parte, las velocidades finales pueden
hallarse a partir de
v = a·t
sin más que sustituir la a de la ecuación anterior
v = (2s/t2)·t = 2s / t
Las velocidades finales
han de ser, por lo tanto, proporcionales a los tiempos, y los caminos
recorridos proporcionales a los cuadrados de los tiempos.
Una alternativa es el
análisis de video, que permite obtener de un video las trayectorias, y luego de
éstas la velocidad y aceleración.
MATERIALES:
- Rieles
de aluminio
- Tacos
de madera
- Canicas
- Metro
- Cronómetro
- Rotulador
PROCEDIMIENTO:
- Coloca el riel de aluminio apoyado sobre los tacos de madera con cierta
inclinación.
- Haz una marca en un extremo del riel y mide la distancia hasta el
final.
- Mide la inclinación haciendo el cociente entre la altura vertical de
la que cae la bola y la distancia horizontal que recorre.
- Deja caer una canica desde la marca, grabando con el móvil o el
portátil el movimiento. Repítelo dos veces más.
- Cambia la inclinación añadiendo tacos de madera hasta tener un total
de cinco inclinaciones y tres repeticiones para cada una de ellas.
TAREAS:
- Analiza los videos con Tracker o LoggerPro para obtener la aceleración
en cada movimiento.
- Promedia las aceleraciones de cada repetición para obtener un
aceleración por inclinación.
- Haz una tabla con tus datos.
- Obten del programa un gráfico ejemplo de la posición frente al tiempo,
de la velocidad frente al tiempo y de la aceleración frente al tiempo.
- Haz un gráfico de la aceleración frente a la inclinación.
- Comenta las gráficas obtenidas, comparando lo obtenido con lo previsto
de acuerdo a la teoría.
- Evalúa la exactitud de los tiempos medidos en función de la dispersión
de los mismos. Evalúa la precisión de los datos a partir del ajuste de las
gráficas a las líneas de tendencia.
- Evalúa
el procedimiento en cuanto a precisión y exactitud de los resultados.
Expón detalladamente debilidades y fuentes de error del método y
soluciones para las mismas.
TABLA: distancia frente a tiempo
|
Medidas de la rampa
|
1
|
2
|
3
|
||
|
30
|
0,78
|
0,73
|
0,78
|
0,763333333
|
|
|
60
|
1,22
|
1,41
|
1,25
|
1,293333333
|
|
|
90
|
1,87
|
1,68
|
1,66
|
1,736666667
|
|
|
120
|
2,25
|
2
|
1,97
|
2,073333333
|
|
|
150
|
2,44
|
2,5
|
2,16
|
2,366666667
|
|
|
180
|
2,5
|
2,25
|
2,37
|
2,373333333
|
|
|
210
|
2,41
|
2,34
|
2,38
|
2,376666667
|
|
|
240
|
2,5
|
2,44
|
0,54
|
1,826666667
|
|
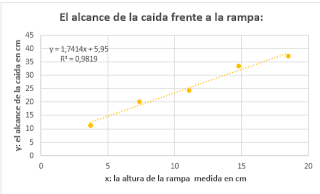
GRÁFICA:
CONCLUSIÓN:
Nuestra conclusión consiste en que mientras
menos distancia menos tiempo tardará en llegar, y mientras más distancia más tiempo
tardará. Esto se debe a que se trata de un movimiento rectilíneo uniformemente
acelerado, por lo tanto, va cogiendo velocidad a medida que cae por dicha
rampa.
EVALUACIÓN:
En este experimento, aunque haya sido corto,
hemos cometido algunos fallos que son los dos siguientes:
Al ser el hierro tan largo hemos tirado la
bolita con una diferencia de 30 cm desde cada distancia, y como ya estaban
marcadas pues no nos habremos dado cuenta de que a lo mejor las distancias no
estaban bien medidas y algunos datos nos han salido mal.
El otro problema que hemos tenido ha sido con
el cronometro que, al tirar la bola, pues cuando ha llegado al final de la
rampa muchas veces mi compañero y yo no hemos estado atentos y no nos ha dado
tiempo de parar el cronómetro cuando ya había llegado la canica, así que esta
podría ser una de las causas por las que tendremos algunos datos mal.
En nuestra opinión pensamos que el experimento
nos ha salido bastante bien, porque solo hay que fijarnos en la gráfica para
ver cómo ha quedado, es decir que todos los datos coinciden perfectamente con
la línea de mejor ajuste.